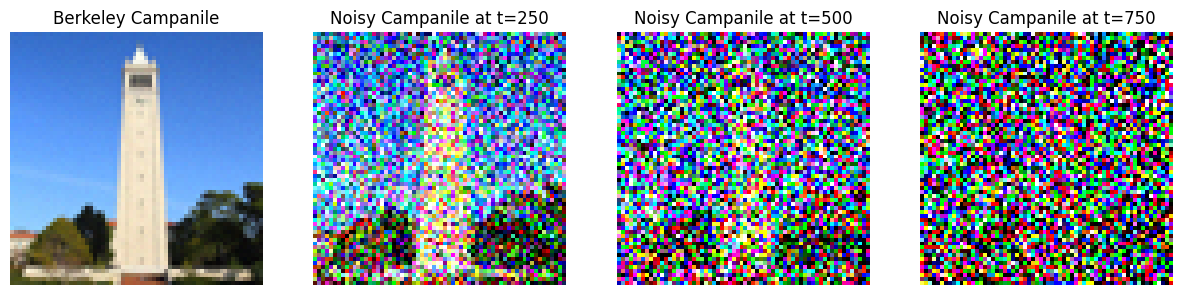
Part A.0: Setup
In the notebook, we instantiate DeepFloyd's stage_1 and stage_2 objects used for generation, as well as several text prompts for sample generation.
For small num_inference_steps, for example, 5, the output fails to provide sufficient
details and contains a lot of noise in the figure. The desciptor from the prompt is poorly reflected
in the output. As we increases num_inference_steps, more details are showcased and
the output better aligns with the content in the prompt.
Random seed I'm using here is 1998.

num_inference_step = 4.
num_inference_step = 20.
num_inference_step = 200.