

Before warping images into alignment, we need to recover the parameters of the transformation between each pair of images. The transformation is a homography: p’=Hp, where H is a 3x3 matrix with 8 degrees of freedom.
$$ \begin{bmatrix} wx' \\ wy' \\ w \end{bmatrix} = H \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$
Where \( H \) is:
$$ H = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & 1 \end{bmatrix} $$
Given a point \( (x, y) \) in the first image and its corresponding point \( (x', y') \) in the second image, the equation can be rearranged to:
$$ h_{11}x + h_{12}y + h_{13} - h_{31}x \cdot x' - h_{32}y \cdot x' = x' $$ $$ h_{21}x + h_{22}y + h_{23} - h_{31}x \cdot y' - h_{32}y \cdot y' = y' $$
To solve for \( H \), computeH constructs a matrix equation \( A \cdot H = b \)
and uses least squares method to find the solution that minimizes the sum of the squared residuals, where:
$$ A = \begin{bmatrix} x & y & 1 & 0 & 0 & 0 & -x \cdot x' & -y \cdot x' \\ 0 & 0 & 0 & x & y & 1 & -x \cdot y' & -y \cdot y' \end{bmatrix} $$
The vector \( b \) is:
$$ b = \begin{bmatrix} x' \\ y' \end{bmatrix} $$
After computing \( H \) from corresponding points from two images, I warp the second image to the first image with forward warping and fill the unmapped pixels
using nearest-neighbor interpolation via warpImage_rec(im, H, polygon = True) The details are:
griddata function with the 'nearest' method is used to interpolate pixel values from the original image to the warped image grid,
ensuring that unmapped pixels are filled accurately.
Two examples of rectified images are shown below:


The goal of this section is to blend two images smoothly by warping the second image into the coordinate of the first image and using a distance transform mask for a gradual transition in the overlapping area of first and second images.
create_distance_transform_mask:
This functions computes the ditance of each pixel from the nearest edge, then normalizes the
distance to the range of 0 and 1.
BlendTwoImages_Distance:
This functions mainly involves: (1) Warp the second image; (2)Create a binary mask to identify overlap area;
(3) Distance transform for alpha blending; (4) Combine the first and second images.





Note: For implementation of part B, I realize the images with more features are better candidates for mosaic. So I've taken more pictures for image processing in this part.


We start with directing using harris corner detection given in harris.py.
In practice,
I find out min_distance=5 and edge_discard=20 gives resonable
number of harris corners in a short time period.
Examples of Harris corners detection are shown below.

To minimize redundant feature corner points, I implement ANMS algorithon[1] as outlined in the function
apply_ANMS. The array radii is initialized as infinite values to store
the mininum suppression radius for each point.
$$ r_i = \min_j \, | \mathbf{x}_i - \mathbf{x}_j |, \quad \text{s.t. } f(\mathbf{x}_i) < c_{\text{robust}} f(\mathbf{x}_j), \quad \mathbf{x}_j \in \mathcal{I} $$
For each corner point, the function iteratively computes \( r_i \). A point i of considers
another point j only if f[i] < c_robust * f[j]. This ensures the weak points
are suppressed if they are near a strong point. The Eculidean distance between points i and
j is calculated and stored as the suppresion radius if it is smaller than the
current value.
Examples of detected Harris corners with ANMS are shown below. In these cases, c_robust = 0.9
and the number of selected points is 500.
[1]Brown, Matthew, Richard Szeliski, and Simon Winder. "Multi-image matching using multi-scale oriented patches." 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). Vol. 1. IEEE, 2005.

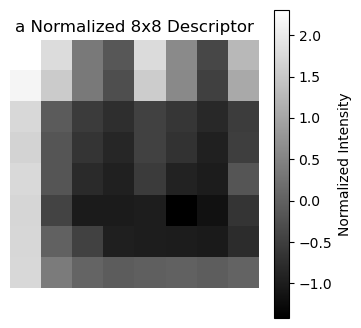
The descriptor function generates descriptors for each selected corners
from the previous parts by extracting the local patches (40x40) around it and downscale it
to 8x8.
It is noted that Gaussian blurring is used here to reduce the noise. Then skimage.transform.resize with
anti_aliasing=True is used. To make the descriptor invariant to intensity, the resized patch is normalized.
The feature_matching function identifies corresponding features between two sets
of the descriptors extracted from images by comparing their similarity using Euclidean distance.
To ensure reliable matches, the function applies Lowe's ratio test. If the distance to the closest
match is significantly smaller (defined by threshold) than the distance to the second-closest
match, the pair of descriptors is considered as a good match.
Output here is a list of matched index pairs representing reliably matched feature points.

However, as shown above, some line pairs indicate incorrect matches that should not be paired. It can be fixed in next section when finding homography.
From lecture note, RANSAC for estimating homography follows the key steps in RANSAC loop
(num_iteration = 1000):
1. Select four feature pairs (at random); 2. Compute homography \( H \) (exact);
3. Compute \( inliers \) where dist(pi', Hpi) < \( \epsilon \); 4. Keep largest
set of inliers; 5. Re-compute least sqaures H estimate on all of the inliers.
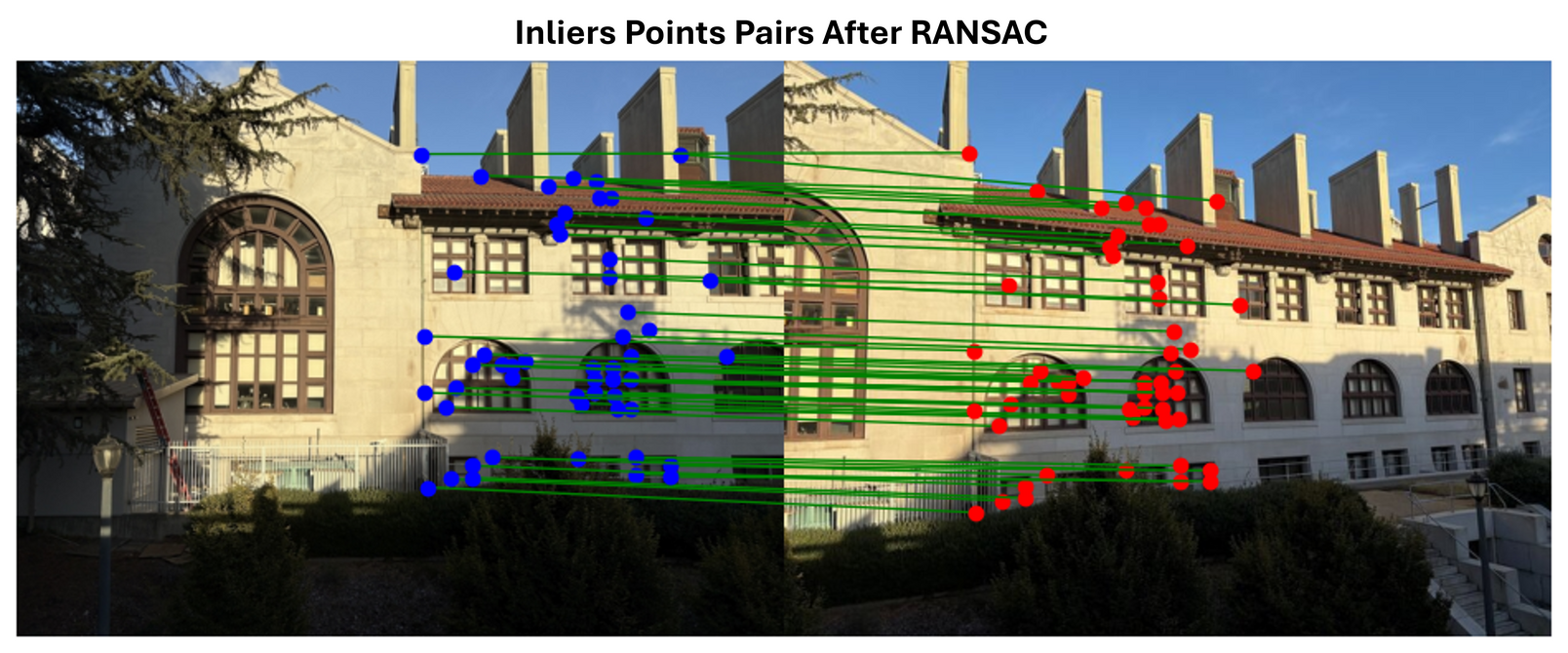
Now we can see that the incorrect pairs have been removed.

More examples:

